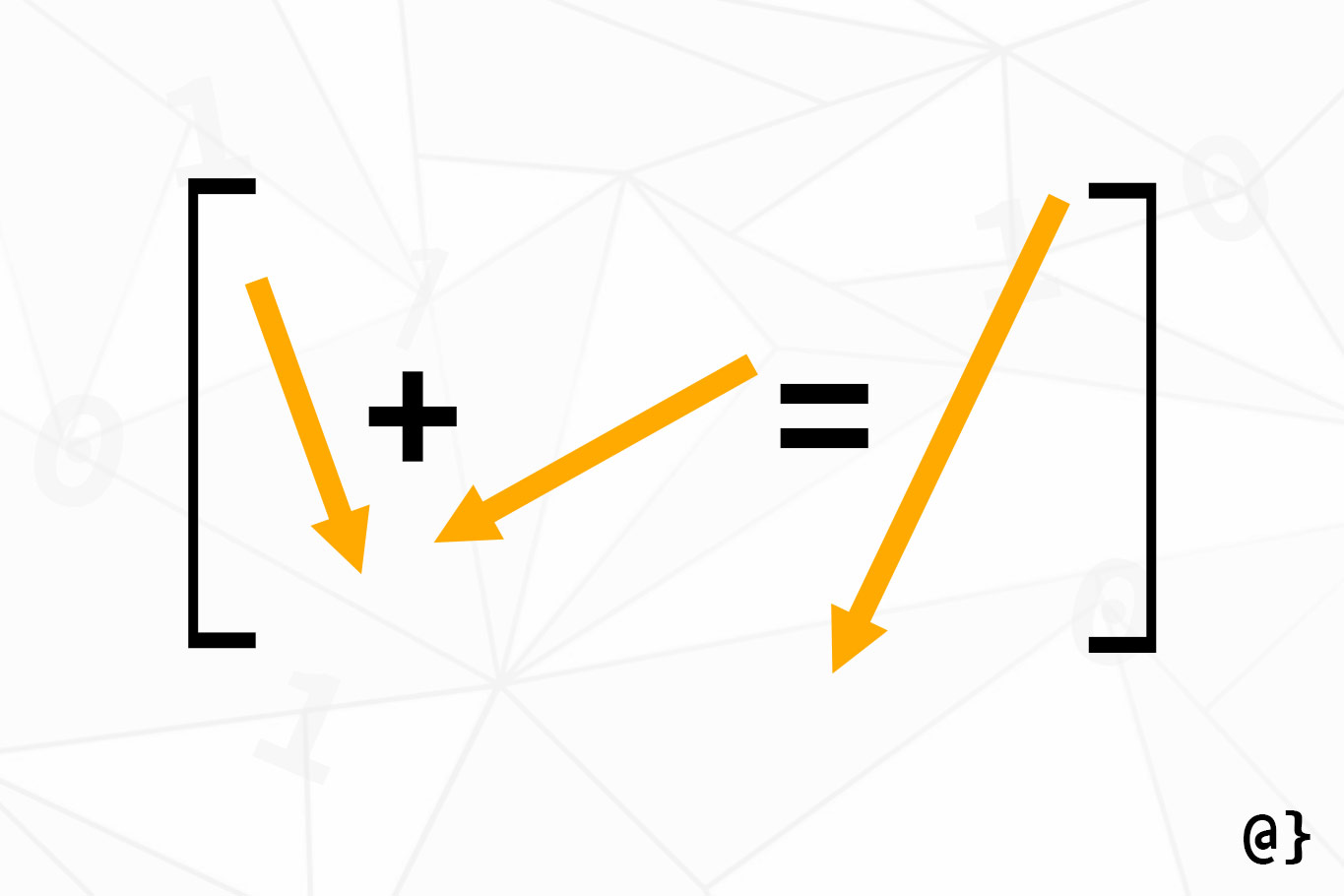Linear algebra has a wide range of applications—from physics, to machine learning, and especially 3D graphics. At the heart of linear algebra are vectors—often referred to as matrices—and the addition of their values. Matrix addition is simple but having some visual aid can help.
The basics of matrix addition don’t stray very far from the basics of the addition we all grew up with. For example 1 + 1 = 2 and [1] + [1] = [2]. Those little brackets? Those denote matrices or vectors depending on the context. Physicists will call them vectors, mathematicians will call the matrices, and computer scientists may just call them lists. I’m going to call them the combined matrix/vector and matrices/vectors to help reinforce the symmetry.
Adding Matrices & Vectors
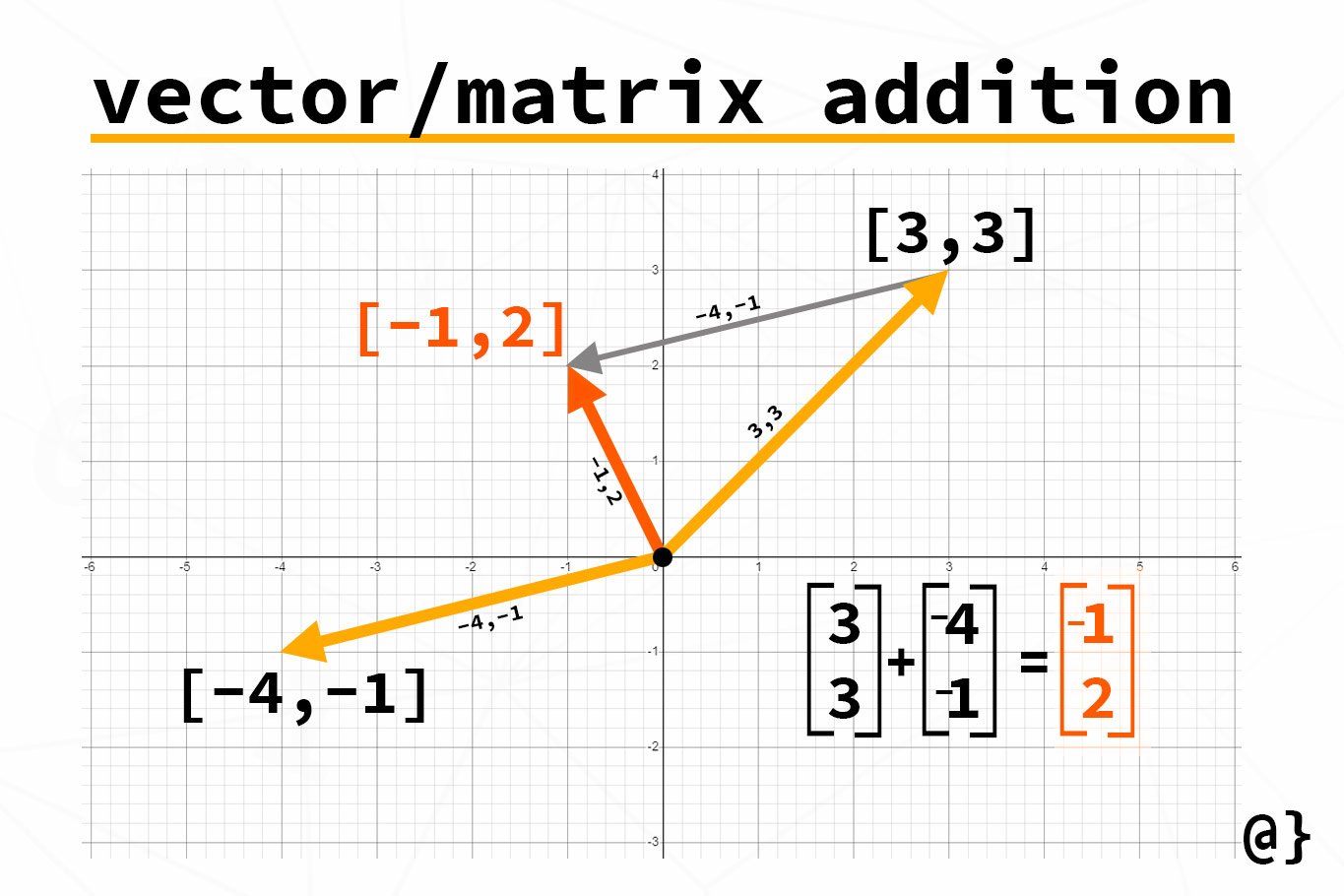
In the illustration above, the term vector gets highlighted as being illustrated as arrows while the term matrix is depicted as a bracketed set of numbers. While helpful, this visual depiction of vectors as arrows is only practical in 2D or 3D space. Not for higher-dimension vectors like [1 4 11 36 9].
In the illustration above, the vectors/matrices [-4, -1] and [3, 3] are being summed. To accomplish this feat, one must add the elements from each matrix/vector in matching order. That means add the first element from the first matrix/vector to the first element in the second matrix/vector. So on and so forth.
This results in the following:
# Adding 1 x 2 matrices/vectors results in a 1 x matrix/vector [3, 3] + [-4, -1] = [(3 + -4), (3 + -1)] = [-1, 2]
If you’re thinking there would be a conundrum should vectors/matrices have a different number of elements you’re right! The following operations aren’t possible:
# Trying to add a 3 x 1 matrix to a 1 x 3 matrix [[2], [4], [6]] + [1, 3, 5] # 2 + 1 = 3 # 4 + ? = x # 6 + ? = x # Trying to add a 1 x 3 matrix to a 3 x 1 matrix [1, 3, 5] + [[2], [4], [6]] # 1 + 2 = 3 # 3 + ? = x # 5 + ? = x # Trying to add a 1 x 3 matrix to a 1 x 4 matrix [1, 3, 5] + [2, 4, 6, 8] # 1 + 2 = 3 # 3 + 4 = 7 # 5 + 6 = 11 # ? + 8 = x
These operations are depicted as they would be in programming languages like Python but depict the same matrix/vector concepts discussed thus far. The takeaway: matrices/vectors can only be added if they have the same dimensions. If you don’t remember anything else—remember that!
Not So Simple
Thus far, we’ve discussed matrix/vector addition as an almost synonymous operation. There are some finer points of study in which separating the terms may be prudent. For an idea of some deeper additive operations, check out the following:
Final Thoughts
Matrices/Vectors are useful tools in many fields of computer science, such as computing gradient descent and other linear regressions within the field of machine learning. These tools allow computers to process conceptually complex problems in a simplified and efficient computational space.
That means big problems can get solved with less computational overhead! Knowing the basics of these operations can help offer insight into the fundamental designs of many of the most complex computational tasks facing science today.