Understanding PyTorch’s Linear Model’s Bias Parameter

Among PyTorch’s many powerful machine learning tools is its Linear model that applies a linear transformation to input values using weights and biases. Practically, this is used to construct neural network layers — sometimes called a “Fully Connected” layer model. It accepts several arguments for network dimensions but also one for “bias.” Here we take a look at what this parameter controls, what are the implications within a network, and why it defaults to a value of True.

Highlights

• Crash course on Linear neural network models
• Understanding network weights and biases
• Bias and added network expressiveness
• When Bias might be a bad thing
• Bias value use in network design
• PyTorch’s Linear Model example code

TL;DR – It enables bias values within the network and defaults to True which is probably what you want.

Crash Course: The Linear Model

Deep learning makes use of multi-layer architectures inspired by the connectivity of neurons in the human brain. Essentially, this involves “nodes” and “layers” of a network such that all nodes in Layer A connect to all nodes in Layer B where Layer A precedes Layer B in calculations. This is a very vanilla model sometimes called a Multi-Layer Perceptron and, more accurately, a multi-layer feedforward network. Generally, this requires at least 3 layers:

• Input Layer
• Hidden Layer
• Output Layer

However, there are often multiple hidden layers and much more complex architectures in modern models such as Recurrent Neural Networks (RNN), Convolutional Nural Networks (CNN), and multi-attention head models like Transformers. For now, the only other concepts we need to know are weights and biases, and activation function:

• Weights are the numerical values associated with the connections between nodes (the lines in the image below) that are multiplied against the input values.
• Biases are values that get added to the product of the weight and the input values
• Activation Function – applied to the weighted sum of the input and bias (e.g. ReLU) often clamping into positive terms.

Each of these components is relevant on a per-node level. That is; each node of a neural network is fed an input that is multiplied by a weight, added a bias, and fed into an activation function before being passed to the next node (usually). Below is a very simple fully-connected deep neural network, illustrating a four-layer fully-connected deep neural network:

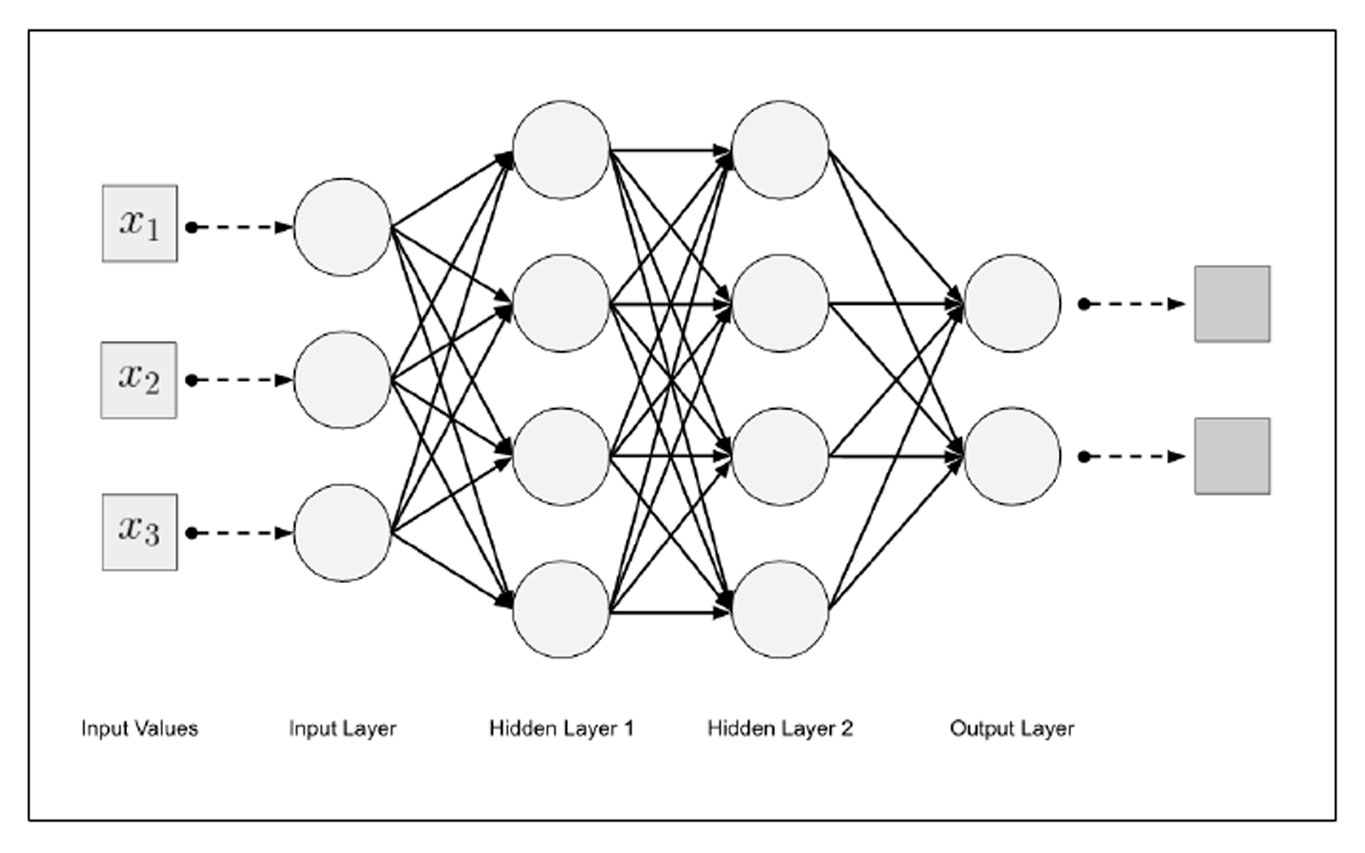
In practice, there can be billions or even trillions of nodes in a layer. In the remainder of this article, we’ll discuss the Bias component, and how PyTorch’s Linear model handles its dynamics. You needn’t have deep PyTorch experience or familiarity to follow along but I don’t know why you’d be reading this if you didn’t.

PyTorch Linear Model

To utilize a PyTorch Linear model (equivalent to one “layer” in the above image) one can import this class as such:

# conventional PyTorch import syntax
import torch.nn as nn

# creates the layer
linear_layer = nn.Linear(
    in_features=3,
    out_features=4,
    bias=True
)

print(linear_layer)

Linear(in_features=3, out_features=4, bias=True)

Here we see a Linear layer being created to mimic the input layer of the image above. There are 3 inputs (X1, X2, X3) and four outputs — one for each node of the Hidden Layer 1. Now, to the focus of our discussion: note the bias argument. This is not a required parameter and is set to True if omitted. The docstrings describe the bias argument as such:

If set to False, the layer will not learn an additive bias. Default: True

Not very helpful if one doesn’t already understand the thing. Let’s break it down a bit into important concepts:

• Layers
• Biases
• Additive (the nature of the bias application here)
• Defaults

Bias in Neural Networks

In neural networks, each neuron has a weight and a bias. The weight determines the strength of the connection between neurons, while the bias allows the neuron to have an output even when all its inputs are zero. Mathematically, the output y of a neuron is calculated as:

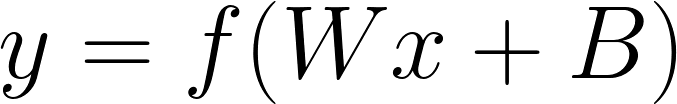
Where:

• $W$ is the weight matrix.
• $x$ is the input vector.
• $b$ is the bias vector.
• $f$ is the activation function.

The bias the parameter in PyTorch’s nn.Linear determines whether or not the layer should have bias terms. If bias=True (default), the layer will have trainable bias terms. If bias=False, no bias terms will be used.

Importance of Bias

Bias isn’t just a performance consideration but essential to the dynamics of neural networks and training. The bias allows the weights (learning of the network) to have another dimension of expression. When multiplied across all layer nodes, this is a powerful increase in overall network expressiveness that, in many cases, leads to better model fitting and performance.

Note: For advanced readers check out the article Reconciling Modern Machine Learning Practice and the Classical Bias-Variance Trade-Off for an interesting discussion about the role of bias in modern model fitting compared to traditional variance-based performance analysis.

Generally, you want to use bias. This is so much the case that PyTorch developers elected to make this parameter default to True. In other words, unless you have a specific reason not to use bias PyTorch is going to use bias. However, there are some cases where bias might be considered unwanted:

1. Normalization Techniques: When using certain normalization techniques, like Batch Normalization, the bias term might become redundant. Batch Normalization already shifts the activations, so an additional bias might not be necessary.
2. Reducing Parameters: Excluding bias can slightly reduce the number of trainable parameters in the model. This can be beneficial in scenarios where there’s limited training data or a need to minimize the model size.
3. Zero-centered Data (mean subtraction): If the input data is zero-centered and pre-processed in a way that the model does not require any additional shift in the activation, then the bias term might not add significant value. Note: zero-centering is a

Aside: Zero Centered Data

“Zero-centered” refers to data that has an average (or mean) value of zero. In the context of neural networks and deep learning, it’s often beneficial to preprocess the data so that its mean is zero. This helps in improving the convergence speed during training and can lead to better model performance.

For example: imagine a dataset with values ranging from 10 to 20. If we subtract the mean (which is 15 in this case) from every data point, the new range would be from -5 to 5, making the data zero-centered. Note: zero-centering data is often used alongside other pre-processing steps such as normalization (scaling) of data.

Full Implementation

The syntax used above for the linear layer makes short work of defining the first input layer of the model depicted in the first image. However, that’s not very useful in terms of creating a usable network. PyTorch provides a Sequential the class that let’s one quickly describe a network architecture as such:

# a 4-layer linear model using ReLu activation functions
model = nn.Sequential(
    nn.Linear(3, 4),
    nn.ReLU(),
    nn.Linear(4, 4),
    nn.ReLU(),
    nn.Linear(4, 2)
)

As described by the official PyTorch documentation:

[The Sequential model] “chains” outputs to inputs sequentially for each subsequent module, finally returning the output of the last module. The value a Sequential provides over manually calling a sequence of modules is that it allows treating the whole container as a single module, such that performing a transformation on the Sequential applies to each of the modules it stores (which are each a registered submodule of the Sequential).

This is one case where the documentation does well to describe the use and novelty of the class. One final point I would note is that the activation functions added here are not included by default if not explicitly defined which is unlikely the desired design.

Discussion

PyTorch makes creating neural networks very easy. With a few lines of code, we were able to create an architecture as shown in the initial diagram we discussed. In terms of developer productivity, it’s hard to overstate the novelty of PyTorch or the Sequential model. The bias parameter is, very likely, one that is only discovered when one begins researching a case where its appropriateness might be called into question — such as some of the cases listed above. In most cases, trainable bias is an essential feature for network dynamics and something that is desirable for neural networks and deep learning.